Published on

Building autograd engine (tinytorch) 02

Authors

part 2/n

Let's Write Blackward pass

backward pass is easy barely an inconvenience. steps:

  1. derivative of anyting with it self is 1
  2. backward pass with
  3. op.backward we will get 2 tensors grad
  4. set grad to each node
    def backward(self,grad=None):
        if grad is None:
            grad = Tensor([1.])
            self.grad = grad

        op = self._ctx.op
        child_nodes = self._ctx.args

        grads = op.backward(self._ctx,grad)

        for tensor,grad in zip(child_nodes,grads):
            tensor.grad = grad

we take grad as input defalut None, we will set it to 1 is we get value of grad None. than to op.backward that gives us 2 grads. assiagn each grad to child node nodes.

Let's test it

if __name__ == "__main__":
    x = Tensor([8])
    y = Tensor([5])

    print("Add")
    z = x + y
    print(z)
    z.backward()
    print(f"x: {x} , grad {x.grad}")
    print(f"y: {y} , grad {y.grad}")
    print("="*100)

    print("Mul")
    z = x * y
    print(z)
    z.backward()
    print(f"x: {x} , grad {x.grad}")
    print(f"y: {y} , grad {y.grad}")
    print("="*100)

and output should be something like this


  ~/workspace/tinytorch   master
❯ /home/joey/miniforge3/bin/python /home/joey/workspace/tinytorch/tinytorch.py
Add
tensor([13])
x: tensor([8]) , grad tensor([1])
y: tensor([5]) , grad tensor([1])
=======================================================
tensor([40])
x: tensor([8]) , grad tensor([5])
y: tensor([5]) , grad tensor([8])
=======================================================

Commit c5a9452c0ef0e23363d84cd44cacd362d53f398b

Connecting Graph

Now we can get grad for +,* lets extend it to composite function supoose you have function f(x)=x3+2⋅xf(x) = x^3 + 2 \cdot x you can break it own as 3 step

f(x)=((x⋅x)⋅x)+(2⋅x)f(x) = ((x \cdot x) \cdot x) +( 2 \cdot x)

This in graph will look like this

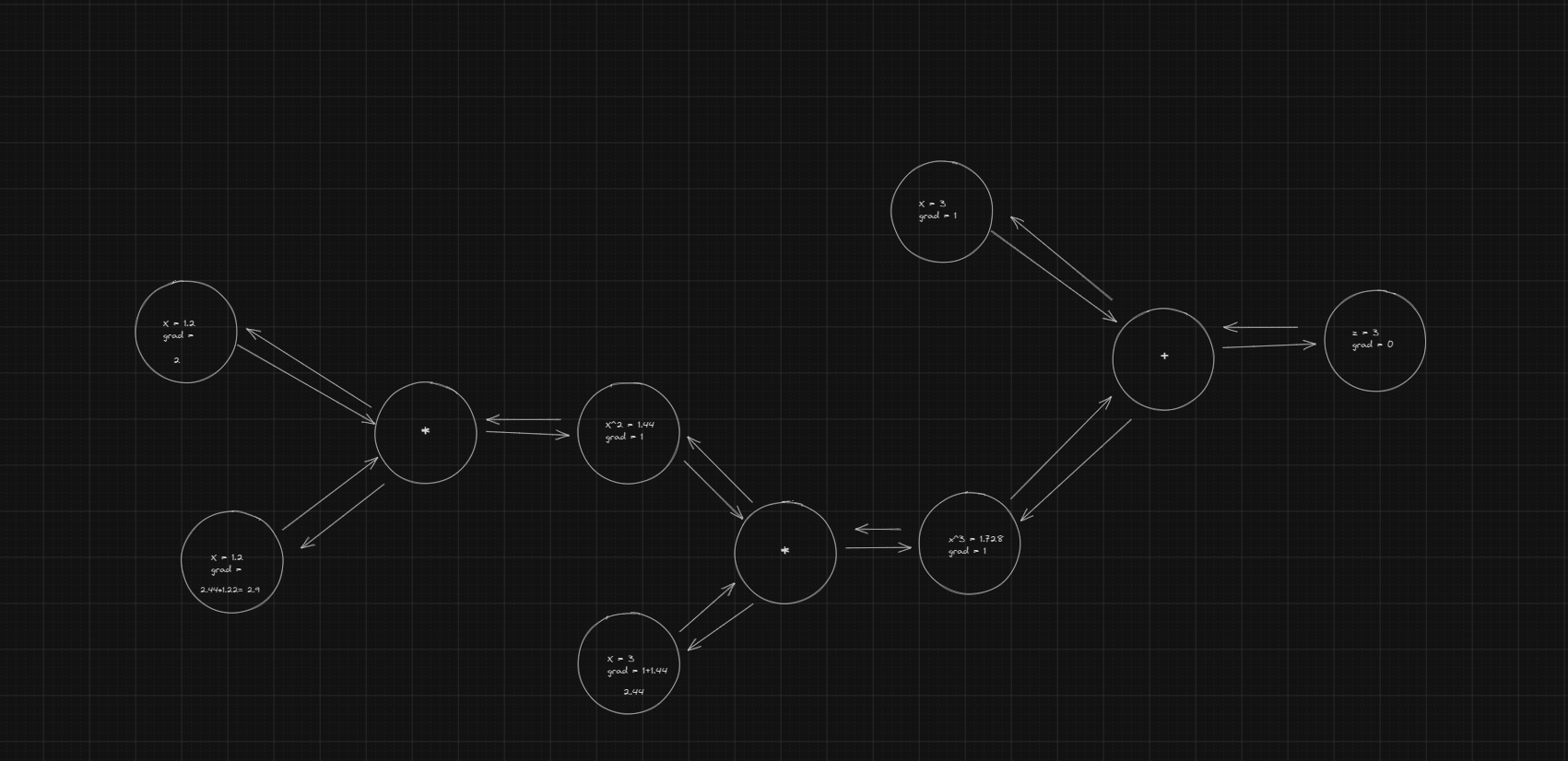
Alt text Alt text

So now we need to pass gradient to previous computaion graph lets modify backward mathoed

    def backward(self,grad=None):
        if self._ctx is None:
            return

        if grad is None:
            grad = Tensor([1.])
            self.grad = grad

        op = self._ctx.op
        child_nodes = self._ctx.args

        grads = op.backward(self._ctx,grad)

        for tensor,grad in zip(child_nodes,grads):
            if tensor.grad is None:
                tensor.grad = Tensor(np.zeros_like(self.data))
            tensor.grad += grad
            tensor.backward(grad)

here we are early return if self._ctx is None that mean we reached at the end of out graph. and now insted of setting grad we init it with zeros (in shape of original). and then we to add grad to it. tensor.grad += grad here we accumulate gradients.

we also need to change Add and Mul method to use upsteam gradient

class Add:
    @staticmethod
    def forward(x, y):
        return Tensor(x.data + y.data)

    @staticmethod
    def backward(ctx, grad):
        x, y = ctx.args
        return Tensor([1])*grad, Tensor([1]) *grad


class Mul:
    @staticmethod
    def forward(x, y):
        return Tensor(x.data * y.data)  # z = x*y

    @staticmethod
    def backward(ctx, grad):
        x, y = ctx.args
        return Tensor(y.data)*grad, Tensor(x.data)*grad #  dz/dx, dz/dy

now we multiplay current grad with upstream grad so they will change accouding to incoming grads

Lets Test it


if __name__ == "__main__":

    def f(x):
        return x*x*x + x

    x = Tensor([1.2])

    z = f(x)
    z.backward()
    print(f"X: {x} grad: {x.grad}")


❯ python tinytorch.py
X: tensor([1.2]) grad: tensor([5.32])

Lets visualize this. now we can calculate gradient at each piont and to backward pass on it. and plot this

derivate of f(x)= x^3+x

in our visulize.py add this code. here we are calculationg grad at each point and ploting it

import graphviz
import matplotlib.pyplot as plt
from tinytorch import *

G = graphviz.Digraph(format="png")
G.clear()


def visit_nodes(G: graphviz.Digraph, node: Tensor):
    uid = str(id(node))
    G.node(uid, f"Tensor: ({str(node.data) }  { 'grad: '+str(node.grad.data) if node.grad is not None else ''}) ")
    if node._ctx:
        ctx_uid = str(id(node._ctx))
        G.node(ctx_uid, f"Context: {str(node._ctx.op.__name__)}")
        G.edge(uid, ctx_uid)
        for child in node._ctx.args:
            G.edge(ctx_uid, str(id(child)))
            visit_nodes(G, child)




def f(x):
    return x * x * x + x
# Defining the function to plot the given function and its derivative using the custom Tensor class
def plot_function_and_derivative():


    # Values for x ranging from -3 to 3
    x_values_custom = np.linspace(-3, 3, 100)
    y_values_custom = []
    derivative_values_custom = []

    # Using the custom Tensor class to calculate the function and its derivative for each x value
    for x_val in x_values_custom:
        x_tensor = Tensor([x_val])
        y_tensor = f(x_tensor)
        y_tensor.backward()
        y_values_custom.append(y_tensor.data[0])
        derivative_values_custom.append(x_tensor.grad.data[0])

    # Plotting the original function and its derivative using the custom implementation
    plt.plot(x_values_custom, y_values_custom, label="f(x) = x^3 + x (custom)")
    plt.plot(x_values_custom, derivative_values_custom, label="f'(x) = 3x^2 + 1 (custom)")

    plt.xlabel('x')
    plt.ylabel('y')
    plt.title('Plot of the Function and its Derivative (Custom Implementation)')
    plt.legend()
    plt.grid(True)
    plt.show()




if __name__ == "__main__":
    plot_function_and_derivative()

    x = Tensor([1.2])
    z = f(x)
    z.backward()
    visit_nodes(G, z)
    G.render(directory="vis", view=True)
    print(f"Z:{x} grad:{x.grad}")

and for referance tinytorch.py

import numpy as np


class Tensor:
    def __init__(self, data):
        self.data = data if isinstance(data, np.ndarray) else np.array(data)
        self.grad = None
        self._ctx = None


    def __add__(self, other):
        fn = Function(Add, self, other)
        result = Add.forward(self, other)
        result._ctx = fn
        return result

    def __mul__(self, other):
        fn = Function(Mul, self, other)
        result = Mul.forward(self, other)
        result._ctx = fn
        return result

    def __repr__(self):
        return f"tensor({self.data})"

    def backward(self,grad=None):
        if self._ctx is None:
            return

        if grad is None:
            grad = Tensor([1.])
            self.grad = grad

        op = self._ctx.op
        child_nodes = self._ctx.args

        grads = op.backward(self._ctx,grad)

        for tensor,grad in zip(child_nodes,grads):
            if tensor.grad is None:
                tensor.grad = Tensor(np.zeros_like(self.data))
            tensor.grad += grad
            tensor.backward(grad)


class Function:
    def __init__(self, op, *args):
        self.op = op
        self.args = args


class Add:
    @staticmethod
    def forward(x, y):
        return Tensor(x.data + y.data)

    @staticmethod
    def backward(ctx, grad):
        x, y = ctx.args
        return Tensor([1])*grad, Tensor([1]) *grad


class Mul:
    @staticmethod
    def forward(x, y):
        return Tensor(x.data * y.data)  # z = x*y

    @staticmethod
    def backward(ctx, grad):
        x, y = ctx.args
        return Tensor(y.data)*grad, Tensor(x.data)*grad #  dz/dx, dz/dy




if __name__ == "__main__":

    def f(x):
        return x*x*x + x

    x = Tensor([1.2])

    z = f(x)
    z.backward()
    print(f"X: {x} grad: {x.grad}")

graphvis computation graph

derivate of f(x)= x^3+x

commit f1fb4c1b7b0ea51d270651337c600a2a3cabe267

( ˶ᵔ ᵕ ᵔ˶ ) Discuss on Twitter