This is a micro dev blog on how to build a micro Jax / mlx-like transformation engine, because I don't find anything easy that explains function transformation engines on the internet. Just like Karpathy-senpai's micrograd is a simple version of PyTorch, microjax is a simpler version of Jax.

Github: microjax - leave a ⭐ if you find this useful.
Notebook: learn step by step 😉
DM me on twitter @shxf0072 if you have any questions/corretions.

Warning: This is made for understanding with incrementally increasing complexity, not absolute correctness.

Now there exits Autodidax, but its pretty hard, with heavy words and lambda functions.

I had idea bcs of this :3, hance microjax

Way back, Google was TensorFlow-pilled. Google has a custom chip TPU and XLA, a really smart linear algebra compiler to make it go brr, but TensorFlow was awful to work with. Other growing frameworks like PyTorch had a dynamic nature that wasn't that great. Jax was an experimental project from Google that converts Python traces to XLA, which can be compiled with MLIR and run on accelerators like GPUs and TPUs. We can divide Jax into two parts: function transformation and XLA compiler. Function transformation gives us the ability to calculate gradients, Hessians, and define vmap-like transformations, while XLA IR conversion gives us speed. Here we will only cover a simple function transformation engine, so the X part of Jax is not here, but hey, MLX has X so I don't care, I'm calling it microjax. Although Jax has gone more mainstream recently, the story of Jax goes back to autograd.

Autograd had a more novel goal. You need to calculate gradients for machine learning or scientific computing, and Python is the language of scientific computing. So let's make Python differentiable, but how can one make a high-level, interpreted language like Python differentiable?

By writing an interpreter, of course!

Base Interpretor

first we will start primitive, this are fundameation ops in jax land all all other oprator will be base on it, btw this is scalr valued only so its more easy to understand, (np array are techincally supported but i will not define array ops for simplicity)

from __future__ import annotations

import math
from contextlib import contextmanager
from typing import Any, Callable

class OPS:
    ADD = "add"
    MUL = "mul"
    NEG = "neg"
    RECIP = "recip"
    EXP = "exp"
    SIN = "sin"
# ik i can make this enum, i choose not too :P

add

You only need this ops for most this, you can define your own if that tickles your fancy

Lets start with base interpretor, this is like abstract class,

class Interpreter:
    def __init__(self, level: int = 0, *args, **kwargs):
        self.level = level

    def process_primitive(self, prim, boxes, params):
        "in this function, either you process primitives or you unbox and send to lower level interpreter"
        raise NotImplementedError

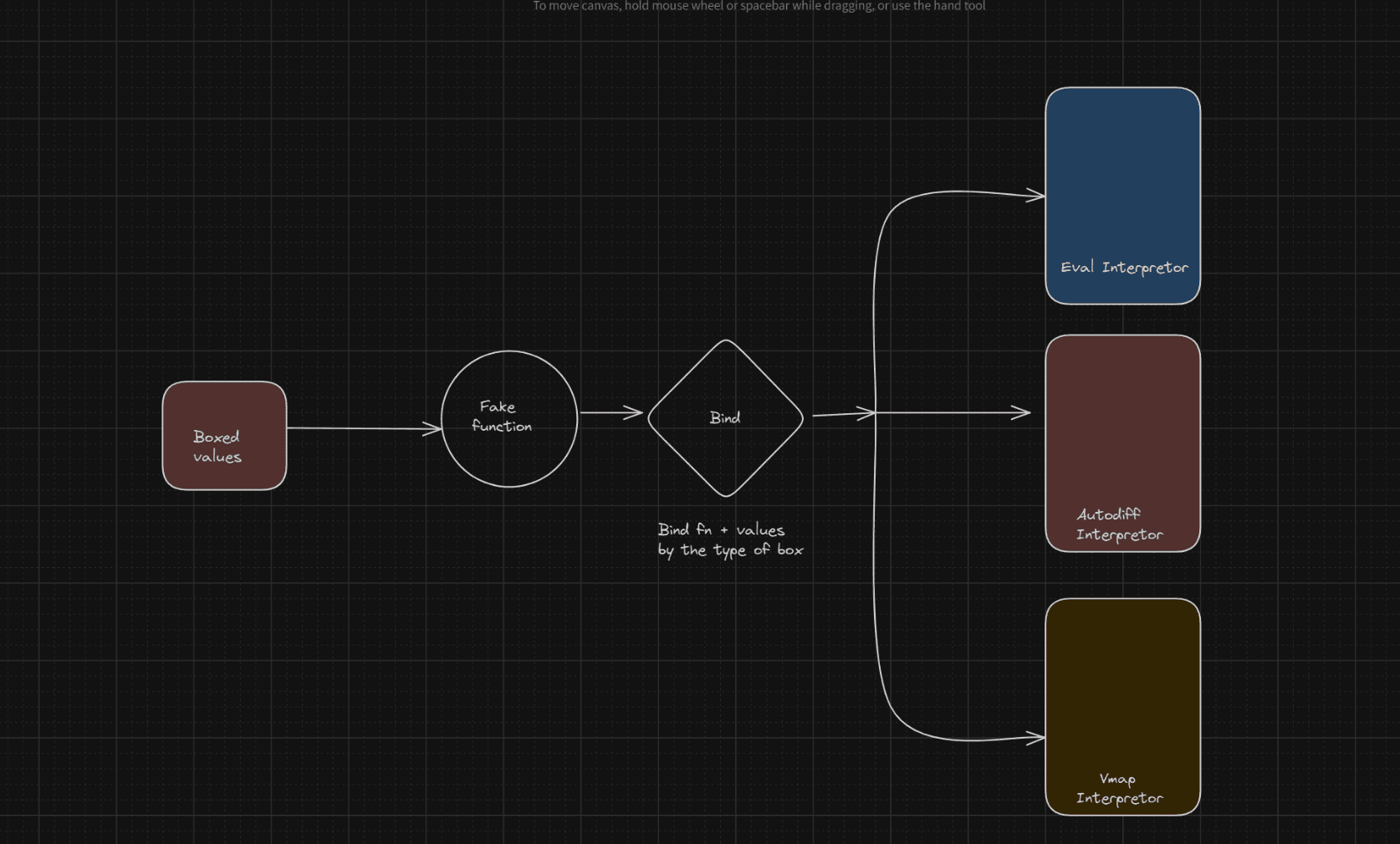
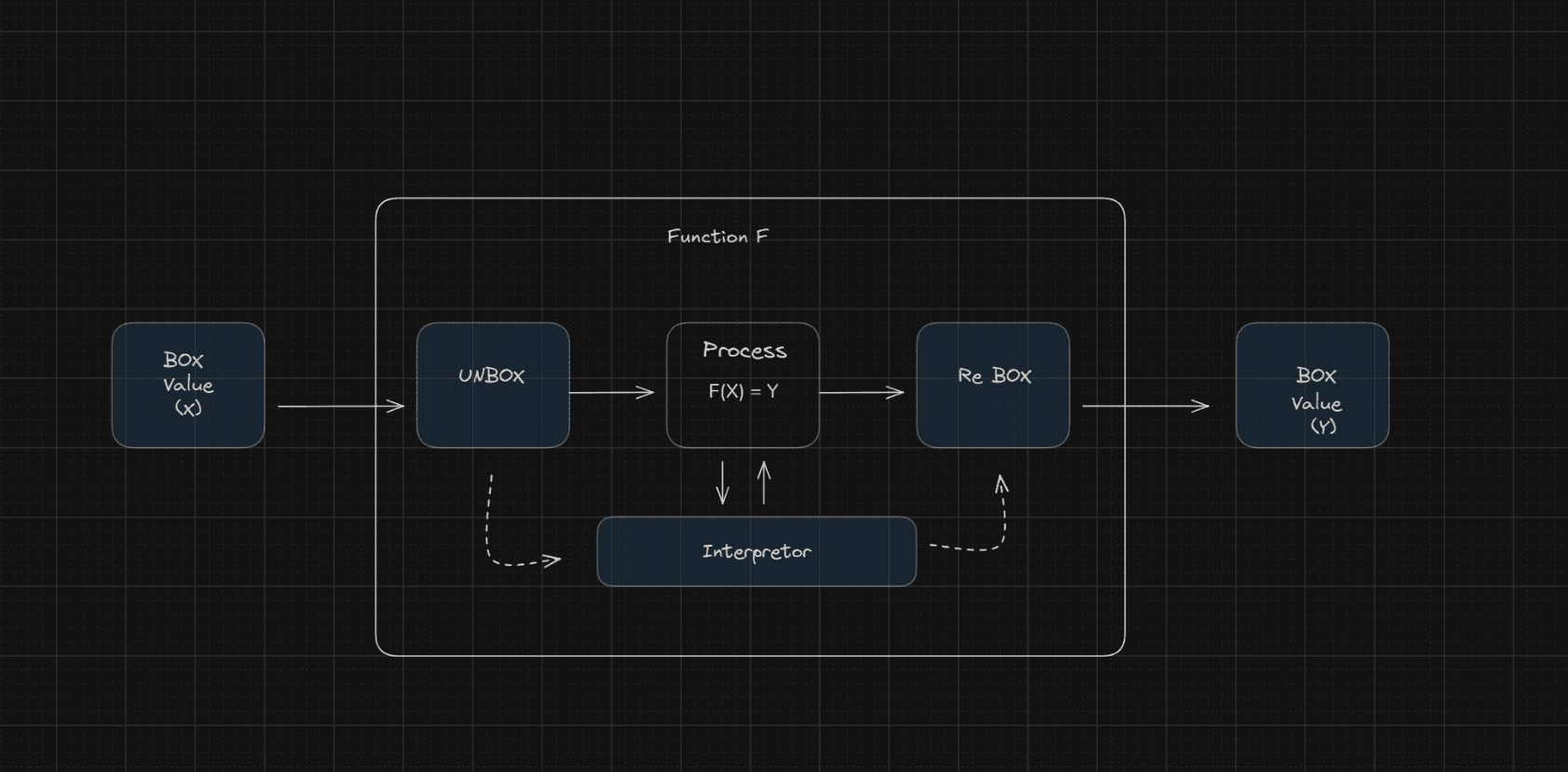
In JAX, this is called a Trace. A Trace keeps track of tracers, which are simply boxed values. We put values in boxes along with some extra information like whether we need to calculate gradients or other things like shape and which interpreter to use. For each unique type of transformation, we will have a box of that type and an interpreter of that type.

Now we will have multiple interpreters. To know in which context the boxed values should evaluate, we need to keep track of interpreters. We will do that with the most common data structure: stack.

STACK: list[Interpreter] = []


def push_interpreter(interpreter: Interpreter):
    STACK.append(interpreter)
    return STACK


def pop_interpreter() -> Interpreter:
    return STACK.pop()


@contextmanager
def interpreter_context(interpreter_type: Interpreter):
    stack_item = interpreter_type(level=len(STACK))
    push_interpreter(stack_item)
    try:
        yield stack_item
    finally:
        pop_interpreter()

Now let's define Box, Box (tracer) is what actually flows through functions you define. We need to override some dunder methods to make it work with Python.

class Box:
    _interpreter: Interpreter

    def aval(self):
        raise NotImplementedError

    def __add__(self, other):
        return add(self, other)

    def __radd__(self, other):
        return add(other, self)

    def __mul__(self, other):
        return mul(self, other)

    def __rmul__(self, other):
        return mul(other, self)

    def __neg__(self):
        return neg(self)

    def __sub__(self, other):
        return add(self, neg(other))

    def __rsub__(self, other):
        return add(other, neg(self))

    def __truediv__(self, other):
        return mul(self, recip(other))

    def __rtruediv__(self, other):
        return mul(other, recip(self))

    def __iadd__(self, other):
        return add(self, other)

    def __imul__(self, other):
        return mul(self, other)

    def __isub__(self, other):
        return add(self, neg(other))

    def __itruediv__(self, other):
        return mul(self, recip(other))

# dont worry about this undefined functions, we add them later

we are almost done with abstract classes just few helper

when function recives multiple boxed values, we need to find top level interpreter for them,

def find_top_interpreter(args):
    """
    find the top level interpreter for the given arguments
    """
    interpreters = []
    for item in args:
        if isinstance(item, Box):
            interpreters.append(item._interpreter)

    if interpreters:
        return max(interpreters, key=lambda x: x.level)

    # if no interpreters are found, return the default EvalInterpreter
    return STACK[0]

if one values in box at level 2 and another at level 3, we need to raise them to level 3, with this function

def full_raise(interpreter: Interpreter | Any, out) -> Box | JVPBox:
    """
    if interpreter need values boxed
    if out is not boxed, box it (using interpreter.pure)
    ie. raise out to the box level
    """
    if not isinstance(out, Box):
        return interpreter.pure(out)
    return out

Each boxed value will have an interpreter assigned to it. Each interpreter will have a level indicating its position in the stack. The find_top_interpreter function will find the highest level interpreter among them all. full_raise will raise up a value to the current interpreter level in the stack. bind_single is just a small wrapper to handle the tuple returned by bind.

def bind(prim, *args, **params):
    interpreter = find_top_interpreter(args)
    
    # this will raise the boxes to the top level
    # eg converts primitive values to Boxes if interpreter is not the top level
    boxes = [full_raise(interpreter, arg) for arg in args]
    
    outs = interpreter.process_primitive(prim, boxes, params)
    
    return [out for out in outs]


def bind_single(prim, *args, **params):
    (out,) = bind(prim, *args, **params)
    return out

bind is importent function, which will call interpreters

Primitives

These are building blocks, all other functions will build on top of these. I like to call them mock functions as they don't really compute anything; they are more like routers for boxes to interpreters.

def add(*args):
    return bind_single(OPS.ADD, *args)

def mul(*args):
    return bind_single(OPS.MUL, *args)

def neg(x):
    return bind_single(OPS.NEG, x)

def recip(x):
    return bind_single(OPS.RECIP, x)

def exp(x):
    return bind_single(OPS.EXP, x)

def sin(x):
    return bind_single(OPS.SIN, x)

Primitives are like mock functions. When you call mul(Box1(3), Box1(2)), this will find interpreters for Box1(3) and Box1(2), then find the interpreter with the highest level among them. It will unbox these values and tell that interpreter to process those primitives. For every op type, there is a primitive op function.

Composite functions build on top of primitives. As long as you can express your function in terms of primitives, you can use arbitrarily complicated functions.

def cos(x):
    return sin(x + math.pi / 2)

def sigmoid(x):
    return 1 / (1 + exp(-x))

def tanh(x): 
    return 2 * sigmoid(2 * x) - 1

def silu(x):
    return x * sigmoid(x)

Eval Interpreter

Even if we have nice abstraction layers, at the end someone has to run add or mul functions. This will be done by the eval interpreter. We will first define evaluation rules and then the eval interpreter.

class EvalRules:
    def __init__(self):
        self.rules = {
            OPS.ADD: self.add,
            OPS.MUL: self.mul,
            OPS.NEG: self.neg,
            OPS.RECIP: self.recip,
            OPS.EXP: self.exp,
            OPS.SIN: self.sin,
        }

    def __getitem__(self, op):
        return self.rules[op]

    def add(self, primals, *args):
        x, y = primals
        return [x + y]

    def mul(self, primals, *args):
        x, y = primals
        return [x * y]

    def neg(self, primals, *args):
        (x,) = primals
        return [-x]

    def recip(self, primals, *args):
        (x,) = primals
        return [1 / x]

    def exp(self, primals, *args):
        (x,) = primals
        return [math.exp(x)]

    def sin(self, primals, *args):
        (x,) = primals
        return [math.sin(x)]

We don't expect any boxed values to be passed to the eval interpreter, so we can just call functions directly on values. It's straightforward: take args and return the result.

class EvalInterpreter(Interpreter):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.rules = EvalRules()

    def pure(self, val):
        return val

    def process_primitive(self, prim, values, params):
        return self.rules[prim](values, *params)

Basic interpreter is EvalInterpreter, Now we run run basic program, since evalution are end of primitive we will push eval interpreter at bottom of stack,

push_interpreter(EvalInterpreter())

Now we can kick off basic program,

def func(x):
    return sin(x)*exp(x) + tanh(x)

x = 3.14

func(x)

1.033056645880499

you may feel like this ^ but this abstractions will be used to build more complex AD

Automatic diff

Suppose we have function

y = D(C(B(A(x))))

if x is a vector then its gradient is can be computed by jacobian matrix

\frac{\partial y}{\partial x} = J \cdot v

if you dont know what is jacobian matrix, its just a matrix of partial derivatives, watch is for if need refresh link

Now we can define our function in terms of primitives.

y = D(c), \quad c = C(b), \quad b = B(a), \quad a = A(x)

same way we can define jacobian matrix as product of derivatives of each function, or mathematically we can define big jacobian by chain rule.

F'(x) = \frac{\partial y}{\partial x}

\frac{\partial y}{\partial x}= \frac{\partial y}{\partial c} \cdot \frac{\partial c}{\partial b} \cdot \frac{\partial b}{\partial a} \cdot \frac{\partial a}{\partial x}

$\frac{\partial y}{\partial c} = D'(c) \quad \frac{\partial c}{\partial b} = C'(b) \quad \frac{\partial b}{\partial a} = B'(a) \quad \frac{\partial a}{\partial x} = A'(x)$

So if you multiply jacobian with vector you will get gradient

F'(x) = \frac{\partial y}{\partial x} = \left[\frac{\partial y}{\partial x_1} \cdots \frac{\partial y}{\partial x_n}\right]

You might now from your linear algebra class that if you multiplion is associative, so we mutiply this jacobian chain from any side you want,

\frac{\partial y}{\partial c} \cdot \left(\frac{\partial c}{\partial b} \cdot \left(\frac{\partial b}{\partial a} \cdot \left(\frac{\partial a}{\partial x}\right)\right)\right) = \left(\left( \left( \frac{\partial y}{\partial c} \right) \cdot \frac{\partial c}{\partial b}\right) \cdot \frac{\partial b}{\partial a}\right) \cdot \frac{\partial a}{\partial x}

This equality holds true because matrix multiplication is associative.

Jacobian-Vector Product (JVP)

The Jacobian-Vector Product, or forward-mode autodiff, computes the product of the Jacobian matrix and a vector:

\text{JVP} = J \cdot v

Where $J$ is the Jacobian matrix and $v$ is a vector.

In the context of our chain rule example:

JVP = \frac{\partial y}{\partial c} \cdot \left(\frac{\partial c}{\partial b} \cdot \left(\frac{\partial b}{\partial a} \cdot \left(\frac{\partial a}{\partial x} \cdot v \right)\right)\right)

JVP propagates derivatives forward through the computational graph, from inputs to outputs.

we can cacluating gradient in same direction as function evaluation A->B->C->D , dA->dB->dC->dD

Vector-Jacobian Product (VJP)

The Vector-Jacobian Product, or reverse-mode autodiff, computes the product of a vector and the Jacobian matrix:

\text{VJP} = v^T \cdot J

Where $v^T$ is the transpose of vector $v$ and $J$ is the Jacobian matrix.

In the context of our chain rule example:

VJP = \left(\left(\left(v^T \cdot \frac{\partial y}{\partial c}\right) \cdot \frac{\partial c}{\partial b}\right) \cdot \frac{\partial b}{\partial a}\right) \cdot \frac{\partial a}{\partial x}

VJP propagates derivatives backward through the computational graph, from outputs to inputs. This is the basis for the backpropagation algorithm commonly used in training neural networks.

Forward Mode Autodiff (JVP)

forward mode auto diff really easy. we will box values and its derivative (init 1). as we calculate function in forward direction we will also calculate its derivative.

class JVPBox(Box):
    def __init__(self, interpretor: Interpreter, primal, tangent) -> None:
        super().__init__()
        self._interpreter = interpretor
        self.primal = primal
        self.tangent = tangent
    
    def __repr__(self):
        return f"JVPBox (primal={self.primal}, tangent={self.tangent})"

values is called primal and its derivative is called tangent.

when you have function f(x) = sin(x) its derivate is denoted by slope of tangent line at that point. as each point slopes changes this changes are define by gradient function. so although we get derivative of sin(x) at primal point x by using cos(x) we call it tangent. it suppose to indicate slope of tangent line at that point.

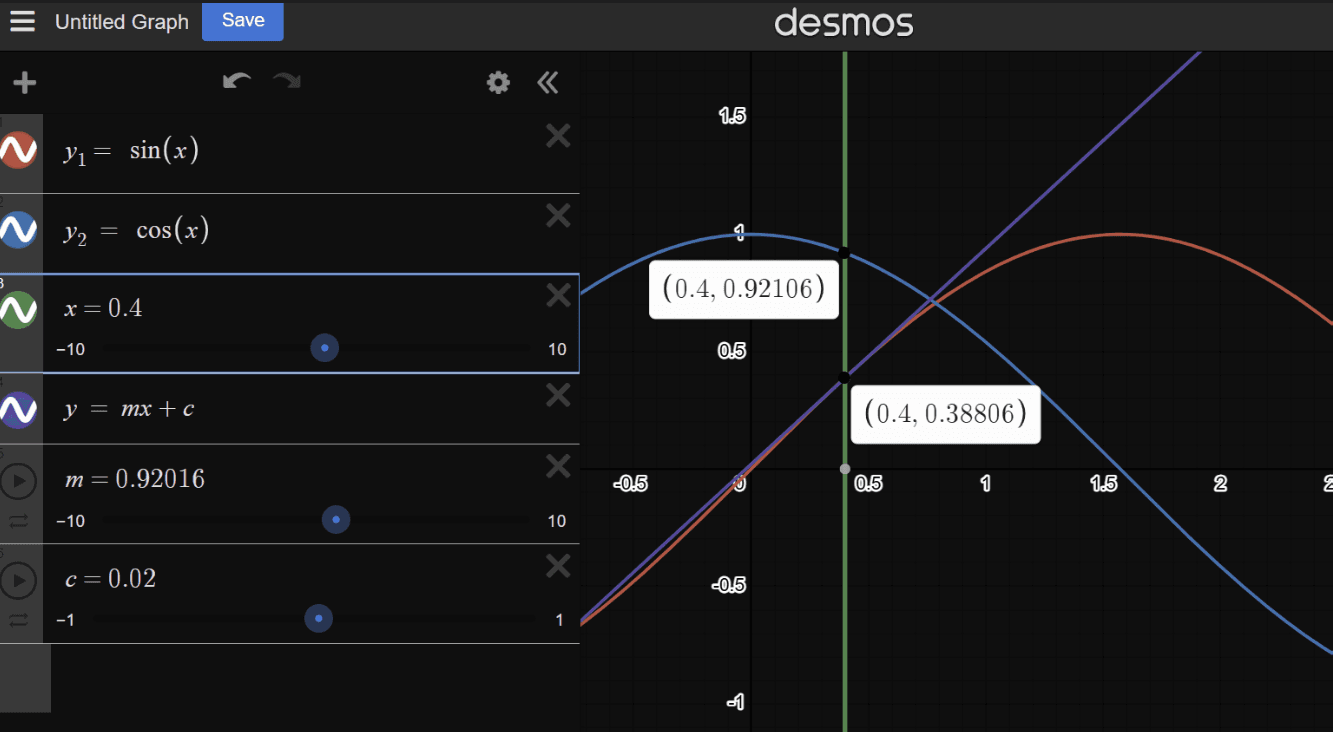
We will define rules for each primitive operation.

note now to define this rule you can only use primitive function, so whole operation need to be closed under composition. eg only on cos define above not math.cos(x)

class JVPRules:
    def __init__(self):
        self.rules = {
            OPS.ADD: self.add,
            OPS.MUL: self.mul,
            OPS.NEG: self.neg,
            OPS.RECIP: self.recip,
            OPS.EXP: self.exp,
            OPS.SIN: self.sin,
        }

    # dont forget to return tuple(primals),tuple(tangents)
    def __getitem__(self, op):
        return self.rules[op]

    @staticmethod
    def add(primals, tangents):
        (x, y), (x_dot, y_dot) = primals, tangents
        return (x + y,), (x_dot + y_dot,)

    @staticmethod
    def mul(primals, tangents):
        (x, y), (x_dot, y_dot) = primals, tangents
        return (x * y,), (x_dot * y + x * y_dot,)

    @staticmethod
    def neg(primals, tangents):
        (x,), (x_dot,) = primals, tangents
        return (-x,), (-x_dot,)

    @staticmethod
    def recip(primals, tangents):
        (x,), (x_dot,) = primals, tangents
        y = 1 / x
        return (y,), (-y * y * x_dot,)

    @staticmethod
    def exp(primals, tangents):
        (x,), (x_dot,) = primals, tangents
        y = exp(x)
        return (y,), (y * x_dot,)

    @staticmethod
    def sin(primals, tangents):
        (x,), (x_dot,) = primals, tangents
        return (sin(x),), (cos(x) * x_dot,)

JVP Interpreter

Now for our first real interpreter. We are boxing values and its tangent. at first we will unbox values, and process this primals and tangents. then we will box the result.

class JVPInterpreter(Interpreter):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.rules = JVPRules()

    def pure(self, val):
        return JVPBox(self, val, 0.0)

    def process_primitive(self, prim, boxes, params):
        # unbox values
        primals = [box.primal for box in boxes]
        tangents = [box.tangent for box in boxes]
        
        # process primitive
        op = self.rules[prim]
        primals_out, tangents_out = op(primals, tangents, **params)

        # box values
        result = []
        for p, t in zip(primals_out, tangents_out):
            result.append(JVPBox(self, p, t))
            
        return result

jvp simple is function that takes function and its input and its tangent and return the function output and its tangent.

def jvp_simple(func, primals, tangents):
    with interpreter_context(JVPInterpreter) as iptr:
        box_in = [JVPBox(iptr, x, t) for x, t in zip(primals, tangents)]
        out = func(*box_in)
        box_out = full_raise(iptr, out)
        primal_out, tangent_out = box_out.primal, box_out.tangent
    return primal_out, tangent_out


def func(x):
    return sin(x) + exp(x)

x,xdot = 3.14,1

y,y_dot = jvp_simple(func, (x,), (xdot,))

print(y,y_dot)

23.10545951163867 22.103868126994644

Now lets define wrapper function that will take function. modify inputs do the jvp and return the gradient.


def deriv(function):
    def jvp_forward(input_value):
        _, gradient = jvp_simple(function, (input_value,), (1,))
        return gradient

    return jvp_forward

def func(x):
    return sin(x) 
x = 3.14

print(func(x))
deriv_func = deriv(func)
print(deriv_func(x))

0.0015926529164868282 -0.9999987317275395

But what will happen if we take derivative of derivative func

deriv_func = deriv(func)
deriv_func2 = deriv(deriv_func)
print(deriv_func2(x))

-0.0015926529164865067

we get double derivative or hessian

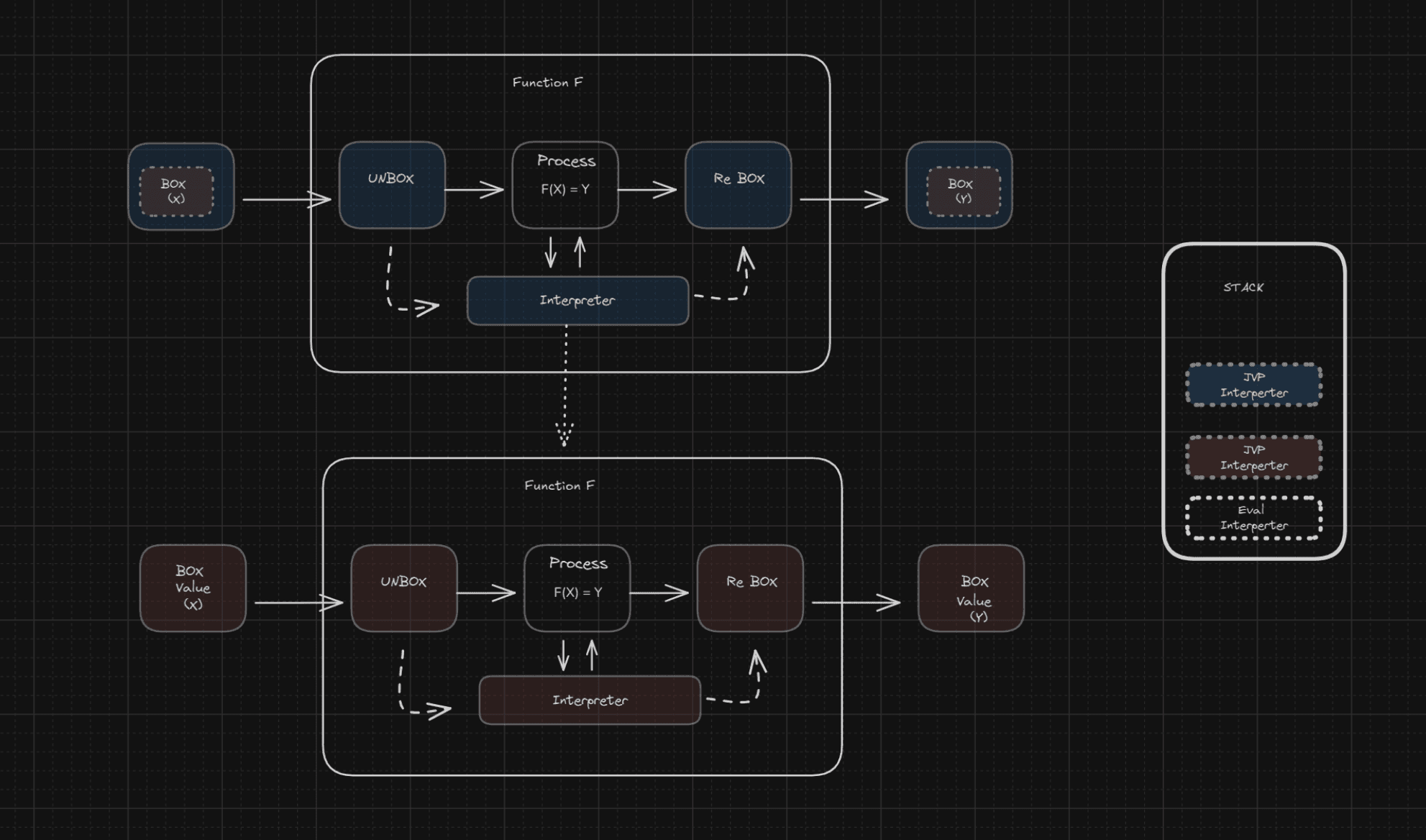
Whats is happening here is we are double boxing values, BOX2( BOX1(primal, derv1), derv2 ), But since function are closed under composition we can compose derv arbaritary many times,

for example, lets take function

f(x) = x \cdot sin(x)

import matplotlib.pyplot as plt
import random
plt.style.use("dark_background")

plt.figure(figsize=(10,5))

def forward(func, vec):
    return [func(x) for x in vec]


x = [i / 10 for i in range(-50, 50)]

def func(x):
    return x*sin(x)

primals = forward(func, x)

# first derivative
f_prime = forward(deriv(func), x)
f_prime2 = forward(deriv(deriv(func)), x)
f_prime3 = forward(deriv(deriv(deriv(func))), x)
f_prime4 = forward(deriv(deriv(deriv(deriv(func)))), x)

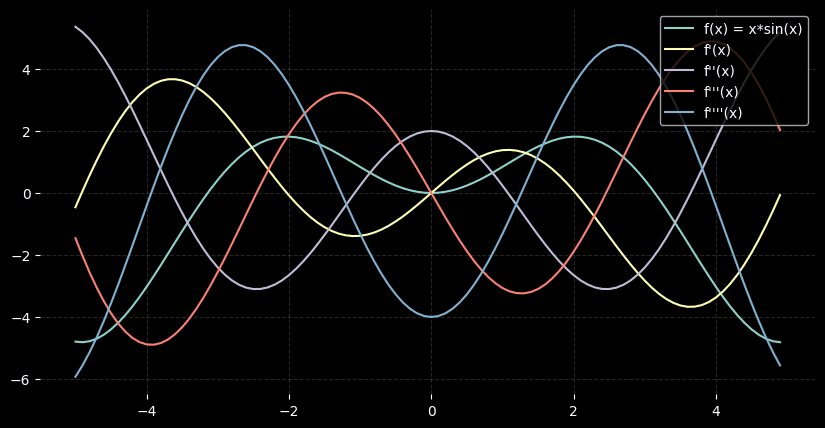
plt.plot(x, primals, label='f(x) = x*sin(x)')
plt.plot(x, f_prime, label="f'(x)")
plt.plot(x, f_prime2, label="f''(x)")
plt.plot(x, f_prime3, label="f'''(x)")
plt.plot(x, f_prime4, label="f''''(x)")

plt.grid(True, linestyle="--", alpha=0.15)
plt.box(False)
plt.legend(loc='upper right')
plt.show()

Reverse Mode Automatic Differentiation (VJP)

In way add added extra infomation via boxing values with tangent in jvp, in vjp we will add extra infomation node. this will create graph that can be traversed in reverse direction. Hance reverse mode autodiff.

Reverse mode autodiff is has good explaination on internet,twitter if flooded with i implimeted auto diff in x. so I wont explain this in detail. best explantion imo is karpathy (senpai) link. what this you will get whats going on here.

define node that will keep backward pass function and its parents nodes

class Node:
    def __init__(self, vjp: Callable, parents: list[Node]) -> None:
        self.vjp = vjp
        self.parents = parents

    @property
    def is_leaf(self):
        return len(self.parents) == 0


def get_leaf_nodes() -> Node:
    return Node(None, [])

rules of backward pass

One important thing to note is that even in backward pass we only call primitive functions that we defined. unlike pytorch where you can do what ever shinanigans you want in backward pass. in jax your backward pass need to closed under composition.

as a result torch is relatively easy to extend (FAFO) while jax is not.



class VJPRules:
    def __init__(self):
        self.rules = {
            OPS.ADD: self.add,
            OPS.MUL: self.mul,
            OPS.NEG: self.neg,
            OPS.RECIP: self.recip,
            OPS.EXP: self.exp,
            OPS.SIN: self.sin,
        }
        """
        Jax define one of vjp or jvp rules
        it derives one from the other 
        but this is much more simple to understand
        """

    def __getitem__(self, op):
        return self.rules[op]

    def add(self, primals):
        x, y = primals

        def vjp_add(grad):
            return grad, grad

        return (x + y,), vjp_add

    def mul(self, primals):
        x, y = primals

        def vjp_mul(grad):
            return grad * y, grad * x

        return (x * y,), vjp_mul

    def tanh(self, primals):
        (x,) = primals
        y = tanh(x)

        def vjp_tanh(grad):
            return ((1 - y * y) * grad,)

        return (y,), vjp_tanh

    def neg(self, primals):
        (x,) = primals

        def vjp_neg(grad):
            return (-grad,)

        return (-x,), vjp_neg

    def recip(self, primals):
        (x,) = primals
        y = 1 / x

        def vjp_recip(grad):
            return (-y * y * grad,)

        return (y,), vjp_recip

    def exp(self, primals):
        (x,) = primals
        y = exp(x)

        def vjp_exp(grad):
            return (y * grad,)

        return (y,), vjp_exp

    def sin(self, primals):
        (x,) = primals
        y = sin(x)

        def vjp_sin(grad):
            return (cos(x) * grad,)

        return (y,), vjp_sin

VJP box where we box primals and its nodes

class VJPBox(Box):
    def __init__(self, interpreter: VJPInterpreter, primal, node: Node) -> None:
        super().__init__()
        self._interpreter = interpreter
        self.primal = primal
        self.node = node
        
    def pure(self,value):
        return VJPBox(self._interpreter, value, get_leaf_nodes())

    def __repr__(self):
        return f"VJPBox (primal={self.primal}, node={self.node})"


class VJPInterpreter(Interpreter):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.rules = VJPRules()

    def pure(self, val):
        return VJPBox(self, val, get_leaf_nodes())

    def process_primitive(self, prim, boxes, params):
        primals_in = [box.primal for box in boxes]
        nodes_in = [box.node for box in boxes]
        op = self.rules[prim]
        primals_out, vjp_out = op(primals_in, **params)
        nodes_out = [Node(vjp_out, nodes_in)]
        result = []
        for p, n in zip(primals_out, nodes_out):
            result.append(VJPBox(self, p, n))
        return result

forward pass will give output and graph, this will be used in backward pass to get the gradient. again watch the karpathy video to get the intuition.


def toposort(end_node):
    def _toposort(seen, node):
        result = []
        if id(node) not in seen:
            seen.add(id(node))
            for p in node.parents:
                result.extend(_toposort(seen, p))
            result.append(node)
        return result

    return reversed([n for n in _toposort(set(), end_node) if n.parents])


def add_grads(grad1, grad2):
    if grad1 is None:
        return grad2
    return grad1 + grad2


def backward_pass(in_nodes, out_node, gradient):
    node_map = {id(out_node): gradient}

    topo_sorted = toposort(out_node)
    for node in topo_sorted:
        node_grad = node_map.pop(id(node))

        input_grads = node.vjp(node_grad)

        for input_grad, parent in zip(input_grads, node.parents):
            parent_id = id(parent)
            node_map[parent_id] = add_grads(node_map.get(parent_id), input_grad)

    return [node_map.get(id(node)) for node in in_nodes]

Now simple VJP function that will take function, add leaf nodes to all inputs and return the output and backward function.


def vjp_simple(func, *args):
    with interpreter_context(VJPInterpreter) as iptr:
        box_in = [VJPBox(iptr, x, get_leaf_nodes()) for x in args]
        out = func(*box_in)
        box_out = full_raise(iptr, out)
        in_nodes = [box.node for box in box_in]
        out_node = box_out.node
        primal_out = box_out.primal

        def func_vjp(grad):
            return backward_pass(in_nodes, out_node, grad)

    return primal_out, func_vjp

grad is small wrapper around vjp

def grad(func):
    def grad_func(*args):
        _, backward = vjp_simple(func, *args)
        return backward(1)[0]

    return grad_func


def func(x):
    # return x*x
    return 3 * x * x * x + 2 * x * x + 2 * x

print(grad(func)(2))
print(grad(grad(func))(2))

46 40

Again you can take arbitrary derivative of function, for example

def func(x):
    return tanh(x)

def forward(func, vec):
    return [func(x) for x in vec]

x = [i / 25 for i in range(-100, 100)]

plt.figure(figsize=(15,8))
primals = forward(func, x)

# first derivative
f_prime = forward(deriv(func), x)
f_prime2 = forward(deriv(deriv(func)), x)
f_prime3 = forward(deriv(deriv(deriv(func))), x)
f_prime4 = forward(deriv(deriv(deriv(deriv(func)))), x)

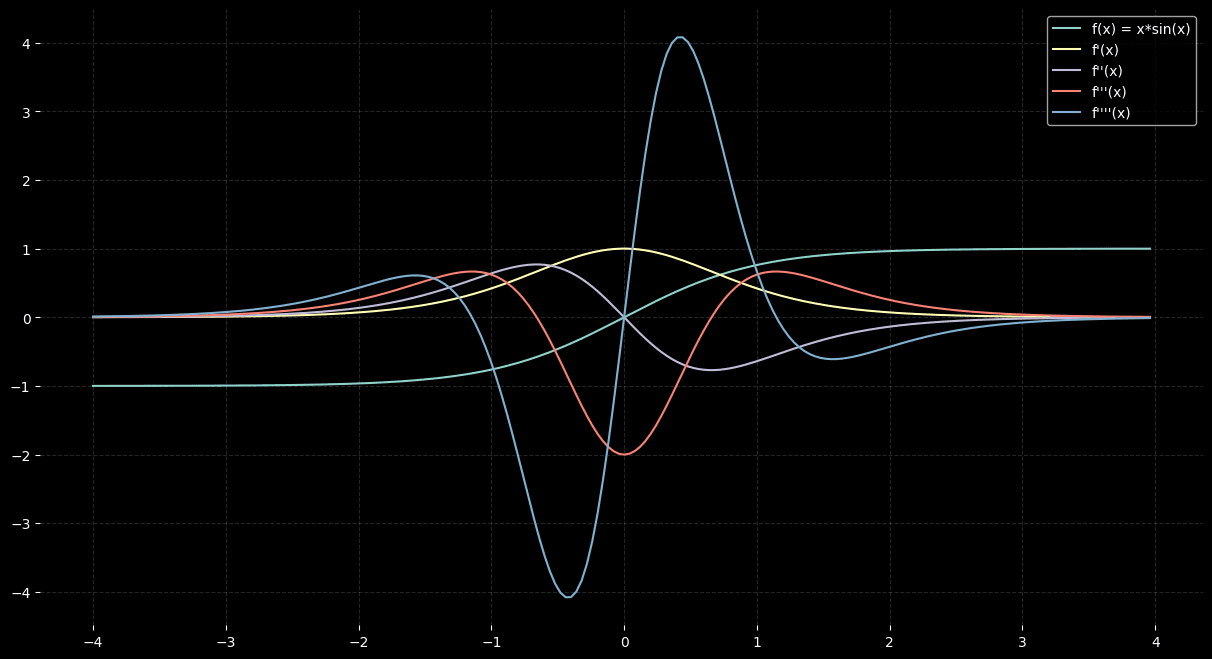
plt.plot(x, primals, label='f(x) = x*sin(x)')
plt.plot(x, f_prime, label="f'(x)")
plt.plot(x, f_prime2, label="f''(x)")
plt.plot(x, f_prime3, label="f'''(x)")
plt.plot(x, f_prime4, label="f''''(x)")

plt.grid(True, linestyle="--", alpha=0.15)
plt.box(False)
plt.legend(loc='upper right')
plt.show()

Function composition

since jvp and vjp are both defined in terms of primitive functions, you can do backward on forward mode autodiff.

def func(x): 
    return sin(x)+ tanh(x)*exp(x)

print("forward on backward")
print(deriv(grad(func))(2))

print("backward on forward")
print(grad(deriv(func))(2))

forward on backward 6.251514736700764 backward on forward 6.251514736700765

Now there is problem you can only pass primitive data types to functions, eg

def func(inputs):
    x,y = inputs
    return tanh(x) + y 

inputs = (6,9)

grad = deriv(func)

#print(grad(inputs))

If you run this you will get error,

      1 def func(inputs):
----> 2     x,y = inputs
      3     return tanh(x) + y

TypeError: cannot unpack non-iterable JVPBox object

we want box values inside inputs list, but here our list is itself boxed Box(list([x,y])) , we need something like [Box(x),Box(y)] enter the pytree.

Pytree

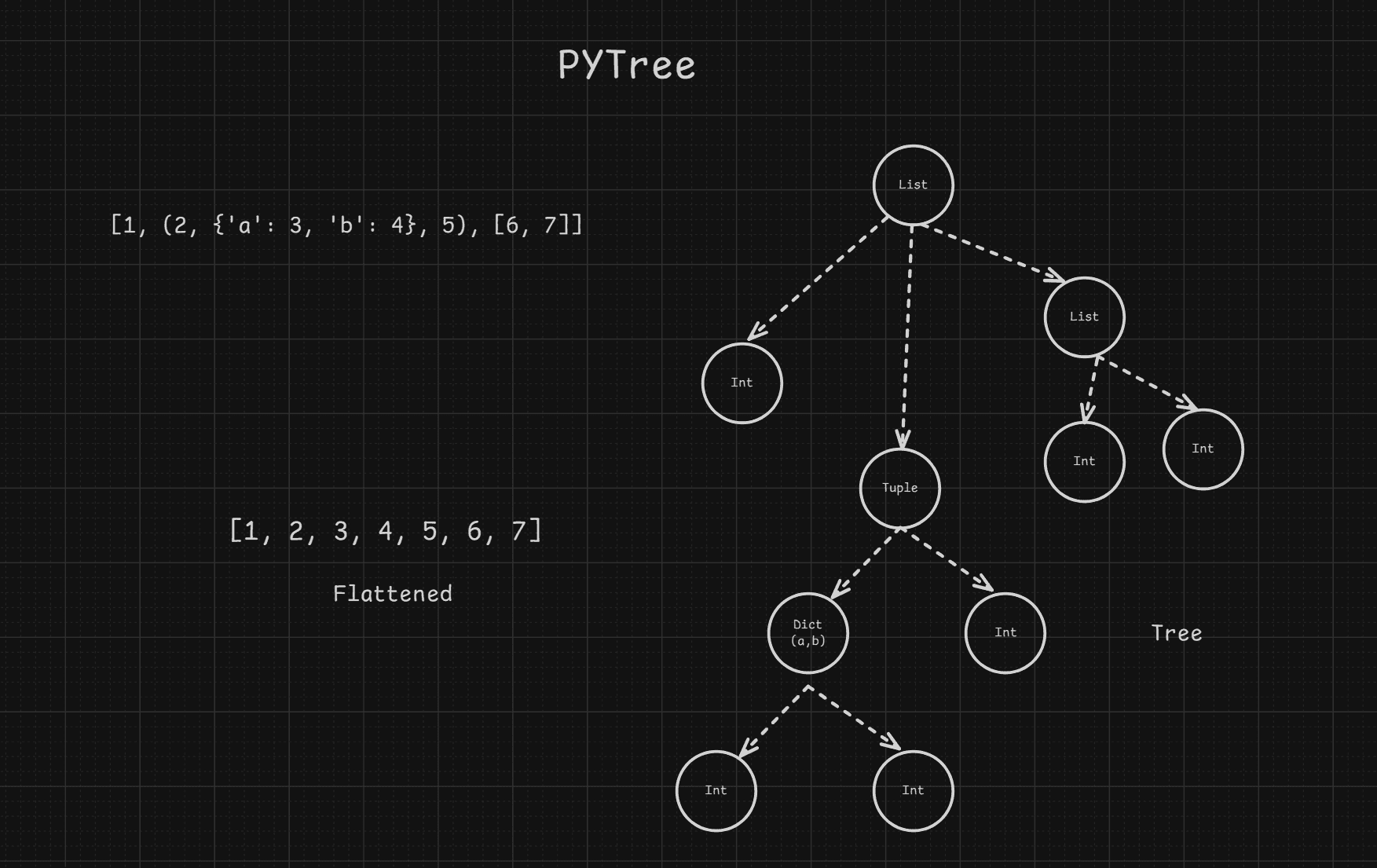
Pytree is a data structure that represents nested data. Its solve problem of boxing and unboxing values. any take any data structure and convert it to flatten and pytree. now this flatten is just list of primitive datatypes so we can loop over them and box it. tree preserve the structure of the data so after boxing values we can reconstruct the original data structure with each values boxed.

from __future__ import annotations

import numpy as np
import numbers

from typing import Any, Hashable, Iterable

PyTreeTypes = list | dict | tuple | Any

Each pytree has a type, metadata and child tree.

type is the type of the data structure, metadata is the data itself and child tree is the child tree of the data structure.


class PyNode:
    def __init__(
        self, node_type: type, metadata: Hashable = None, child_tree: "PyNode" = None
    ):
        self.node_type = node_type
        self.metadata = metadata
        self.child_tree = child_tree

    def __repr__(self):
        s = f"({self.node_type.__name__ if self.node_type !='leaf' else 'leaf'}"
        if isinstance(self.metadata, np.ndarray) or self.metadata:
            s += f":{self.metadata.__class__.__name__}"
        if self.child_tree is not None:
            s += f",{self.child_tree}"
        return s + ")"

    @staticmethod
    def from_iter(pytree) -> tuple[Hashable, "PyNode"]:
        raise NotImplementedError("Not implemented")

    @staticmethod
    def to_iter() -> PyTreeTypes:
        raise NotImplementedError("Not implemented")

    def __eq__(self, other: PyNode) -> bool:
        if self.node_type != other.node_type:
            return False
        if self.child_tree != other.child_tree:
            return False
        return True


class ListNode(PyNode):
    @staticmethod
    def to_iter(lst):
        return None, lst

    @staticmethod
    def from_iter(_, iterable):
        return list(iterable)


class DictNode(PyNode):
    @staticmethod
    def from_iter(keys, vals):
        return dict(zip(keys, vals))

    @staticmethod
    def to_iter(dct):
        keys, values = [], []
        for key, value in sorted(dct.items()):
            keys.append(key)
            values.append(value)
        return keys, values


class TupleNode(PyNode):
    @staticmethod
    def from_iter(_, tup):
        return tuple(tup)

    @staticmethod
    def to_iter(tup):
        return None, tup


node_types: dict[Hashable, PyNode | None] = {
    list: ListNode,
    dict: DictNode,
    tuple: TupleNode,
}

Now we will define tree_flatten and tree_unflatten.

tree_flatten will take any data structure and convert it to flatten and pytree.

tree_unflatten will take flatten list and pytree and convert it to original data structure.


def tree_flatten(x: Any) -> tuple[list[Any], PyNode]:
    def _flatten(x: Any) -> tuple[Iterable, PyNode]:
        data_type = type(x)
        node_type = node_types.get(data_type)
        if node_type is None:
            return [x], PyNode(node_type="leaf", metadata=x, child_tree=None)

        node_metadata, children = node_type.to_iter(x)

        children_flat, child_trees = [], []
        for node in children:
            flat, tree = _flatten(node)
            children_flat.extend(flat)
            child_trees.append(tree)

        subtree = PyNode(
            data_type,  # store the base type instead of the specific node type
            node_metadata,
            tuple(child_trees),
        )
        return children_flat, subtree

    flatten, pytree = _flatten(x)
    return flatten, pytree


def tree_unflatten(flattened_list: list, tree: PyNode) -> Any:
    def _unflatten(flattened_list: list, tree: PyNode) -> Any:
        if tree.node_type == "leaf":
            return next(flattened_list)

        children = []
        for child_tree in tree.child_tree:
            children.append(_unflatten(flattened_list, child_tree))

        node_type = node_types[tree.node_type]
        return node_type.from_iter(tree.metadata, children)

    return _unflatten(iter(flattened_list[:]), tree)




def display_tree(node: PyNode, indent: str = "") -> None:
    if node.node_type == "leaf":
        print(f"{indent}Leaf: {node.metadata}")
    else:
        node_type_name = node.node_type.__name__ if node.node_type != "leaf" else "leaf"
        print(f"{indent}{node_type_name}: {node.metadata}")
        for child in node.child_tree:
            display_tree(child, indent + "    ")


if __name__ == "__main__":
    x = [1, (2, {"a": 3, "b": 4}, 5), [6, 7]]
    flattened, tree = tree_flatten(x)
    print(x)
    print("\nTree structure:")
    display_tree(tree)
    print("\n")
    print("Flattened:", flattened)
    print("\n")

    reconstructed = tree_unflatten(flattened, tree)
    print("\nReconstructed:", reconstructed)
    assert x == reconstructed, "Reconstruction failed"
    print("Reconstruction successful!")


    [1, (2, {'a': 3, 'b': 4}, 5), [6, 7]]
    
    Tree structure:
    list: None
        Leaf: 1
        tuple: None
            Leaf: 2
            dict: ['a', 'b']
                Leaf: 3
                Leaf: 4
            Leaf: 5
        list: None
            Leaf: 6
            Leaf: 7
    
    
    Flattened: [1, 2, 3, 4, 5, 6, 7]
    
    
    
    Reconstructed: [1, (2, {'a': 3, 'b': 4}, 5), [6, 7]]
    Reconstruction successful!

We have way to flatten and unflatten any data structure, now we need to flatten and unflatten function. we will create a function that takes function and pytree and return new function and store. ones you evaluate function it will store the pytree of the functions output.
(simplified: this will convert function to function that takes flatten list and return flatten list)

def flatten_fun(func, in_tree):
    store = {}

    def flat_fun(*args_flat):
        pytree_args = tree_unflatten(args_flat, in_tree)
        out = func(*pytree_args)
        out_flat, out_tree = tree_flatten(out)
        assert len(store) == 0, "Store already has a value!"
        store["tree"] = out_tree
        return out_flat

    return flat_fun, store

Some helper functions


# These functions create nested structures of ones or zeros that match the input structure

def nested_ones_like(item):
    """Create a nested structure of ones with the same shape as the input."""
    if isinstance(item, list):
        return [nested_ones_like(x) for x in item]
    if isinstance(item, tuple):
        return tuple(nested_ones_like(x) for x in item)
    if isinstance(item, dict):
        return {k: nested_ones_like(v) for k, v in item.items()}
    return 1.0 if isinstance(item, numbers.Number) else np.ones_like(item)


def nested_zero_like(item):
    """Create a nested structure of zeros with the same shape as the input."""
    if isinstance(item, list):
        return [nested_zero_like(x) for x in item]
    if isinstance(item, tuple):
        return tuple(nested_zero_like(x) for x in item)
    if isinstance(item, dict):
        return {k: nested_zero_like(v) for k, v in item.items()}
    return 0.0 if isinstance(item, numbers.Number) else np.zeros_like(item)

Now we will reimplement jvp and vjp using pytree. first we will take function as input and flatten it. when we need to evaluate function we will flatten the input and pass it to the function. then we will unflatten the output and return it.


### Refinement of JVP
def jvp_flat(func, primals, tangents):
    with interpreter_context(JVPInterpreter) as iptr:
        tracers_in = [JVPBox(iptr, x, t) for x, t in zip(primals, tangents)]

        outs = func(*tracers_in)

        tracers_out = [full_raise(iptr, out) for out in outs]

        primals_out, tangents_out = [], []
        for t in tracers_out:
            primals_out.append(t.primal)
            tangents_out.append(t.tangent)

    return primals_out, tangents_out


def jvp(func, primals, tangents):
    # Flatten the primals and tangents into flat lists
    primals_flat, in_tree = tree_flatten(primals)
    tangents_flat, in_tree2 = tree_flatten(tangents)
    assert in_tree == in_tree2, "Input trees for primals and tangents must match"

    # Flatten the function f according to the input tree structure
    func_flat, out_tree = flatten_fun(func, in_tree)

    # forward pass
    primals_out_flat, tangents_out_flat = jvp_flat(
        func_flat, primals_flat, tangents_flat
    )

    assert len(out_tree) == 1, "out tree dict must have only one item"
    out_tree: PyNode = out_tree["tree"]

    primals_out = tree_unflatten(primals_out_flat, out_tree)
    tangents_out = tree_unflatten(tangents_out_flat, out_tree)

    return primals_out, tangents_out


def deriv(func, argnums=0):
    if isinstance(argnums, int):
        argnums = [argnums]

    def jvp_forward(*input_value):
        # pass tangent 1 for argnums and 0 for others
        tangents = tuple(
            nested_ones_like(x) if idx in argnums else nested_zero_like(x)
            for idx, x in enumerate(input_value)
        )

        _, gradient = jvp(func, input_value, tangents)

        return gradient

    return jvp_forward

def func(x, y):
    k = tanh(x) * 2.0 + y * y
    z0 = -y + k 
    z1 = y*k
    return {" lets": z0,"f*in":z1, "go!": [x, y]}



print("## pytree.py ##")
x = 3.14
y = 2.71
print(deriv(func, argnums=0)(x, y))


    ## pytree.py ##
    {' lets': 0.01493120808257803, 'f*in': 0.040463573903786465, 'go!': [1.0, 0.0]}

Same for vjp


### Refinement of VJP


def add_grads(grad1, grad2):
    if grad1 is None:
        return grad2
    return grad1 + grad2


def toposort(end_nodes):
    def _toposort(seen, node):
        result = []
        if node not in seen:
            seen.add(node)
            for p in node.parents:
                result.extend(_toposort(seen, p))
            result.append(node)
        return result

    outs = []
    seen = set()
    topo_sorted = []
    for end_node in end_nodes:
        topo_sorted.extend(_toposort(seen, end_node))

    for node in topo_sorted:
        if node.parents:
            outs.append(node)
    result = reversed(outs)
    return list(result)


def backward_pass(in_nodes, out_nodes, gradient):
    node_map = {out_node: g for g, out_node in zip(gradient, out_nodes)}

    topo_sorted = toposort(out_nodes)
    for node in topo_sorted:
        node_grad = node_map.pop(node)

        input_grads = node.vjp(node_grad)

        for input_grad, parent in zip(input_grads, node.parents):
            node_map[parent] = add_grads(node_map.get(parent), input_grad)

    return [node_map.get(node) for node in in_nodes]


def vjp_flat(func, args):
    with interpreter_context(VJPInterpreter) as iptr:
        box_in = [VJPBox(iptr, x, get_leaf_nodes()) for x in args]
        outs = func(*box_in)
        box_out = [full_raise(iptr, o) for o in outs]
        in_nodes = [box.node for box in box_in]
        out_nodes = [box.node for box in box_out]
        out_primals = [box.primal for box in box_out]

        def func_vjp(grad):
            return backward_pass(in_nodes, out_nodes, grad)

    return out_primals, func_vjp


def vjp(func, primals):
    # Flatten the primals and tangents into flat lists
    primals_flat, in_tree = tree_flatten(primals)

    # Flatten the function f according to the input tree structure
    func_flat, out_tree = flatten_fun(func, in_tree)

    # forward pass
    primals_out_flat, vjp_func = vjp_flat(
        func_flat,
        primals_flat,
    )

    assert len(out_tree) == 1, "out tree dict must have only one item"
    out_tree: PyNode = out_tree["tree"]

    primals_out = tree_unflatten(primals_out_flat, out_tree)

    return primals_out, vjp_func


def grad(func, argnums=0):
    if isinstance(argnums, int):
        argnums = [argnums]

    def vjp_func(*input_value):
        result, vjp_func = vjp(func, input_value)

        ones = nested_ones_like(result)
        flat, _ = tree_flatten(ones)
        grads = vjp_func(flat)
        _, in_tree = tree_flatten(input_value)
        grads = tree_unflatten(grads, in_tree)
        grads = tuple(g for idx, g in enumerate(grads) if idx in argnums)
        return grads[0] if len(argnums) == 1 else grads

    return vjp_func


def value_and_grad(func, argnums=0):
    if isinstance(argnums, int):
        argnums = [argnums]

    def vjp_forward(*input_value):
        result, vjp_func = vjp(func, input_value)

        # <hack>
        # jax dont do this nasted ones funnny busniess
        # it just requires output to be scalar
        # but I you can pass one to all output nodes
        # which is effectively like result = sum(result) I dont have redution op
        # basically result.sum().backward() in pytorch
        ones = nested_ones_like(result)
        flat, _ = tree_flatten(ones)
        # </hack>

        # backward pass
        grads = vjp_func(flat)

        output, in_tree = tree_flatten(input_value)
        grads = tree_unflatten(grads, in_tree)

        grads = tuple(g for idx, g in enumerate(grads) if idx in argnums)

        return result, grads[0] if len(argnums) == 1 else grads

    return vjp_forward

Now you can do stuff like this, where you pass state dict and get grad for that state dict, and build complex differentiable program.


def linear(state,inputs):
    weight,bias = state["weights"], state["bias"]
    total = 0
    for w, x in zip(weight, inputs):
        prod = w * x 
        total = total + prod 
    return total + bias

state = {"weights":[1,2,3], "bias": 1}
inputs  = [0.3, 0.5, 0.7]

print(grad(linear)(state,inputs))

    {'bias': 1.0, 'weights': [0.3, 0.5, 0.7]}

value,grads = value_and_grad(linear)(state,inputs)
print(value)
print(grads)

    4.3999999999999995
    {'bias': 1.0, 'weights': [0.3, 0.5, 0.7]}

vmap, pmap and jit

I am not going to cover this, its microjax after all. but to give you intuition, in way we added tangents for jvp and node for vjp, for vmap we box shape infomation, write batching interpreter, and do lambda x: [f(x[0]) for _ in range(x.shape[0])] at rules level, yes its just map. if you do this map parallel you get pmap,

just like we carried info tangent for jit we carry all history of function (graph) and do graph optimization things and compile it to xla. we you 2nd time call jitted function it flows to that optimized graph not your original function. which make it faster.